正弦定理(せいげんていり)

正弦定理(せいげんていり)とは, 三角比の定理の１つで, 「三角形の三辺」と「正弦」の関係のことです。

【教材プリント　無料ダウンロード　問題演習用】

正弦定理 証明 問題プリントダウンロード

正弦定理 証明 解答プリントダウンロード

【数学用語　解説】

用語：正弦定理(せいげんていり)
英語：Law of Sines
別名：サインの定理・三角形の外接円の半径の求め方
解説：正弦定理(せいげんていり)とは、三角比の定理の１つで、「三角形の三辺」と「余弦」の関係のことです。

正弦定理によって、三角形の辺と角から、わからない辺と角を、計算で求められるようになりました。

正弦定理によって、三角形の外接円の半径も、求められるようになりました。

その結果、天文学・地理学・建築学などで、測量の精度が高まりました。





プロ家庭教師の数学教材で、指導歴１０年以上の講師が執筆しています。

【正弦定理　証明問題】

$\triangle$ＡＢＣにおいて

ＢＣ＝$a$
ＣＡ＝$b$
ＡＢ＝$c$

$\angle$ＣＡＢ＝$A$
$\angle$ＡＢＣ＝$B$
$\angle$ＢＣＡ＝$C$

とする。

この時

$\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}$

を証明しなさい。


また $\triangle$ＡＢＣの外接円をＧとし、その半径を $r$ とする。

$\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2r$

を証明しなさい。

【正弦定理　証明問題】

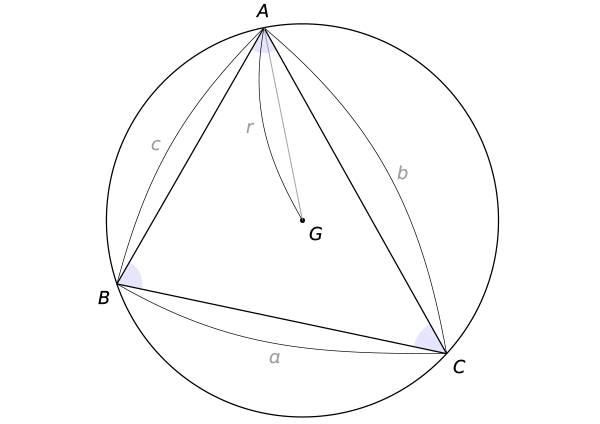
$\triangle$ＡＢＣにおいて

ＢＣ＝$a$
ＣＡ＝$b$
ＡＢ＝$c$

$\angle$ＣＡＢ＝$A$
$\angle$ＡＢＣ＝$B$
$\angle$ＢＣＡ＝$C$

とする。

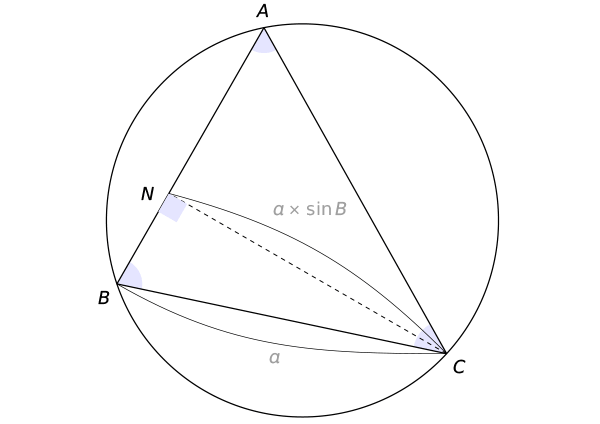
$\triangle$ＡＢＣの点Ｃから、辺ＡＢへ、垂線を引き、交点をＮとする。

$\triangle$ＢＣＮは、直角三角形なので

$ＣＮ=ＢＣ \times \sin B$

$ＣＮ=a \times \sin B$　・・・(１)


また

$\triangle$ＡＣＮは、直角三角形なので

$ＣＮ=ＡＣ \times \sin A$

$ＣＮ=b \times \sin A$　・・・(２)


（１）を（２）へ代入して

$a \times \sin B = b \times \sin A$

$\dfrac{a}{\sin A} = \dfrac{b}{\sin B}$


また

$\triangle$ＡＢＣの点Ｂから、辺ＡＣへ、垂線を引き、交点をＭとする。



$\triangle$ＢＣＭは、直角三角形なので

$ＢＭ=ＢＣ \times \sin C$

$ＢＭ=a \times \sin C$　・・・(３)


また

$\triangle$ＢＡＭは、直角三角形なので

$ＢＭ=ＡＢ \times \sin A$

$ＢＭ=c \times \sin A$　・・・(４)


（３）を（４）へ代入して

$a \times \sin C = c \times \sin A$

$\dfrac{a}{\sin A} = \dfrac{c}{\sin C}$


以上より


$\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C}$


次に

$\triangle$ＡＢＣの外接円をＧとし、その半径を $r$ とする。

線分ＡＧの延長と、外接円Ｇとの交点を、Ｄとする。



$\triangle$ＡＢＤについて

辺ＡＤは、円の直径なので

$\angle$ＡＢＤ＝$90^\circ$

となり、$\triangle$ＡＢＤは直角三角形である。

辺ＡＢ＝辺ＡＤ $\times \sin \angle ＡＤＢ$

$c$ ＝ $2r \times \sin \angle ＡＤＢ$　・・・(５)

円周角の定理より

$\angle$ＡＤＢ＝$\angle$ＡＣＤ＝$C$

（５）に代入すると

$c = 2r \times \sin C$

$\dfrac{c}{\sin C} = 2r$


以上より

$\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2r$

大学受験数学 三角比

大学受験数学

プロ家庭教師