【極限 数列の極限 解説】
数列 $2n-1$ は $1, 3, 5, 7, 9 ・・・$ と増加していくので
$\displaystyle \lim_{ n \to \infty } 2n-1 =\infty$
数列 $3-n^2$ は $2, -1, -6, -13, -22 ・・・$ と減少していくので
$\displaystyle \lim_{ n \to \infty } 3-n^2 =-\infty$
数列 $2+(-1)^n$ は $1, 3, 1, 3, 1 ・・・$ となるので
$\displaystyle \lim_{ n \to \infty } 2+(-1)^n $ は振動する。
数列 $\frac{\Large 1}{\Large n^3}$ は $1, \frac{\Large 1}{\Large 8}, \frac{\Large 1}{\Large 27}, \frac{\Large 1}{\Large 64} ・・・$ と絶対値が減少していくので
$\displaystyle \lim_{ n \to \infty } \frac{1}{n^3}=0$
数列 $\displaystyle 1 - \frac{1}{n}$ は $0, \frac{\Large 1}{\Large 2}, \frac{\Large 2}{\Large 3} ・・・$ と1に近づいていくので
$\displaystyle \lim_{ n \to \infty } 1 - \frac{1}{n} =1$
数列 $\displaystyle \frac{1}{(-2)^n}$ は $-\frac{\Large 1}{\Large 2}, \frac{\Large 1}{\Large 4}, -\frac{\Large 1}{\Large 8} ・・・$ と絶対値が減少していくので
$\displaystyle \lim_{ n \to \infty } \frac{1}{(-2)^n}=0$
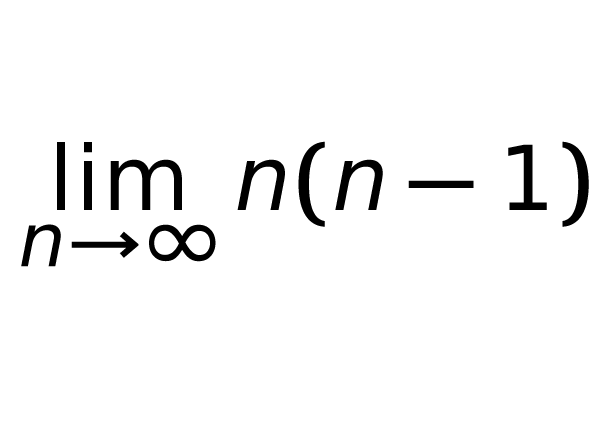

質問と回答