黄金三角形

この記事は、新しい記事へ更新されました。





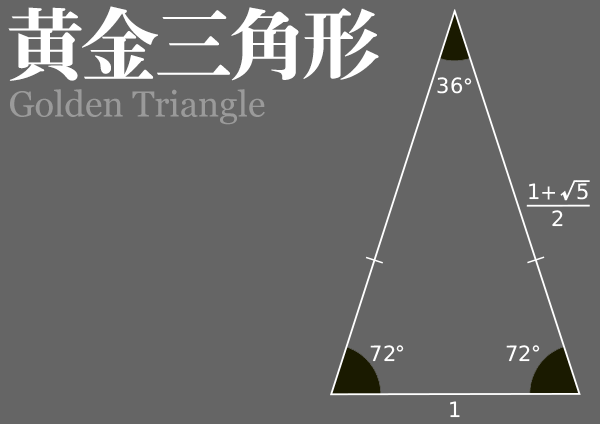
黄金三角形(おうごんさんかくけい)とは、二等辺三角形の１つで、辺の比が、黄金比になる三角形です。

【教材プリント　無料ダウンロード　問題演習用】

黄金三角形 問題プリントダウンロード

黄金三角形 解答プリントダウンロード

【数学用語　解説】

用語：黄金三角形(おうごんさんかくけい)
英語：Golden Triangle
別名：３６度の二等辺三角形・黄金比の三角形
解説：黄金三角形(おうごんさんかくけい)とは、二等辺三角形の１つで、辺の比が、黄金比になる三角形です。

黄金三角形は、頂角３６度・底角７２度の、二等辺三角形です。

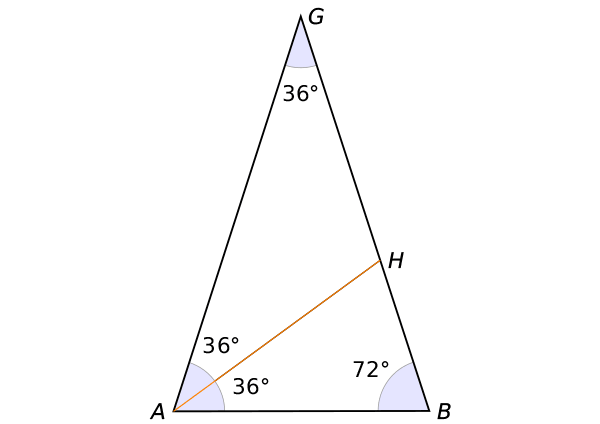
黄金三角形の底角から、角の二等分線を引くと、さらに黄金三角形が現れます。






プロ家庭教師の数学教材で、指導歴１０年以上の講師が執筆しています。

【黄金三角形　解法　角の二等分線】

黄金三角形の底角から、角の二等分線を引いてみましょう。


$\triangle$ＡＢＧは、辺ＡＧ＝辺ＢＧの、黄金三角形です。

底角$\angle$ＢＡＧの、二等分線を引き、辺ＢＧとの交点をＨとします。



$\triangle$ＢＨＡに注目すると

$\angle$ＢＡＨ＝$\angle$ＢＡＧ $\times \frac{\Large 1}{\Large 2}$

＝$36^\circ$　　・・・(１)

また

$\angle$ＡＢＨ＝$72^\circ$　　・・・(２)

また

$\angle$ＢＨＡは、$\triangle$ＡＨＧの外角なので

$\angle$ＢＨＡ＝$\angle$ＨＡＧ＋$\angle$ＨＧＡ

＝$36^\circ$＋$36^\circ$＝$72^\circ$　　・・・(３)


以上の(１)(２)(３)より、

$\triangle$ＢＨＡも黄金三角形となる。

数学図形分野 小テスト 無料ダウンロード 一覧

高校受験数学 図形分野

高校受験数学

プロ家庭教師