共通テスト数学1A 2021年大問1 傾向対策解答解説

数学の教材プリントで、大学入学共通テスト２０２１年の大問１、問題解答ダウンロードです。

オンライン学習用で、生徒・保護者・教員・家庭教師のために、無料ダウンロードを提供します。

【教材プリントダウンロード　演習用】

大学入学共通テスト数学１Ａ　２０２１年大問１　問題ダウンロード

大学入学共通テスト数学１Ａ　２０２１年大問１　解答ダウンロード

【２０２１年大問１】

年度：２０２１年(令和三年)

大問：大問１(必答)

設問	分野	単元
１ー（１）ー（１）	二次方程式	解の公式
１ー（１）ー（２）	二次方程式	解と係数の関係
１ー（１）ー（３）	二次方程式	解と係数の関係
１ー（２）ー（１）	三角比	三角比の計算
１ー（２）ー（２）	三角比	余弦定理
１ー（２）ー（３）	三角比	正弦定理
１ー（２）ー（４）	三角比	正弦定理

【プロ家庭教師　数学１Ａ　対策講座】

数学１Ａの対策カリキュラムを、プロ家庭教師に指導依頼できます。

【２０２１年大問１　（１）】

$c$ を正の整数とする。

$x$ の二次方程式

$2x^2+(4c - 3)x + 2c^2 - c - 11 = 0$　・・・①

について考える。

【２０２１年大問１　（１）ー（１）】

$c = 1$ のとき,　①の左辺を因数分解すると

$($ア$x + $イ$)(x - $ウ$)$

であるから、①の解は

$x= - \dfrac{イ}{ア}, ウ$

である。

【２０２１年大問１　（１）ー（２）】

$c = 2$ のとき,　①の解は

$\dfrac{-エ\pm \sqrt{オカ}}{キ}$

であり、大きい方の解を $\alpha$ とすると

$\dfrac{5}{\alpha}= \dfrac{ク＋ \sqrt{ケコ}}{サ}$

である。

また

$m < \dfrac{5}{\alpha} < m+1$

を満たす整数 $m$ は(　シ　)である。

【２０２１年大問１　（１）ー（３）】

太郎さんと花子さんは, ①の解について考察している。


太郎：①の解は $c$ の値によって, ともに有理数である場合もあれば, ともに無理数である場合もあるね。 $c$ がどのような値のときに, 解は有理数になるのかな。

花子：二次方程式の解の公式の, 根号の中に, 着目すればいいんじゃないかな。


①の解が異なる二つの有理数であるような, 正の整数 $c$ の個数は(　ス　)個である。

【２０２１年大問１　（２）】

$\triangle$ＡＢＣの外側に、辺ＡＢ, 辺ＢＣ, 辺ＣＡをそれぞれを一辺とする正方形ＡＤＥＢ, ＢＦＧＣ, ＣＨＩＡを描き

点Ｅと点Ｆ, 点Ｇと点Ｈ, 点Ｉと点Ｄを、それぞれ線分で結んだ図形を考える。

以下において

ＢＣ＝$a$
ＣＡ＝$b$
ＡＢ＝$c$

$\angle$ＣＡＢ=$A$
$\angle$ＡＢＣ=$B$
$\angle$ＢＣＡ=$C$

とする。

【２０２１年大問１　（２）ー（１）】

$b$＝$6$
$c$＝$5$
$cos A$＝$\dfrac{3}{5}$　のとき

$sin A$＝$\dfrac{(　セ　)}{(　ソ　)}$　であり

$\triangle$ＡＢＣの面積は(　タチ　)

$\triangle$ＡＩＤの面積は(　ツテ　)である。

【２０２１年大問１　（２）ー（２）】

正方形ＢＦＧＣ, ＣＨＩＡ, ＡＤＥＢの面積を

それぞれ　$S_1 ,　S_2 ,　S_3$　とする。

このとき　$S_1-S_2-S_3$　は

$0^\circ < A < 90^\circ$ のとき　(　ト　)

$A=90^\circ$ のとき　(　ナ　)

$90^\circ < A < 180^\circ$ のとき (　二　)


(　ト　)から(　二　)の解答群(同じものを繰り返し選んでもよい)

解答番号０.　$0$である
　　
解答番号１.　正の値である

解答番号２.　負の値である

解答番号３.　正の値も負の値もとる

【２０２１年大問１　（２）ー（３）】

$\triangle$ＡＩＤ, $\triangle$ＢＥＦ, $\triangle$ＣＧＨの面積を

それぞれ　$T_1 ,　T_2 ,　T_3$　とする。

このとき(　ヌ　)である。


(　ヌ　)の解答群

解答番号０.　$a < b < c$ ならば $T_1 > T_2 > T_3$
　　
解答番号１.　$a < b < c$ ならば $T_1 < T_2 < T_3$

解答番号２.　$A$ が鈍角ならば $T_1 < T_2$ かつ $T_1 < T_3$

解答番号３.　$a,　b,　c$　の値に関係なく $T_1=T_2=T_3$

【２０２１年大問１　（２）ー（４）】

$\triangle$ＡＢＣ, $\triangle$ＡＩＤ, $\triangle$ＢＥＦ, $\triangle$ＣＧＨのうち

外接円の半径が最も小さいものを求める。

$0^\circ < A < 90^\circ$ のとき　

ＩＤ(　ネ　)ＢＣ であり

$\triangle$ＡＩＤの外接円の半径(　ノ　)$\triangle$ＡＢＣの外接円の半径

であるから, 外接円の半径が最も小さい三角形は

$0^\circ < A < B < C < 90^\circ$ のとき(　ハ　)である

$0^\circ < A < B < 90^\circ < C$ のとき(　ヒ　)である


(　ネ　)と(　ノ　)の解答群(同じものを繰り返し選んでもよい)

解答番号０.　$<$
　　
解答番号１.　$=$

解答番号２.　$>$


(　ハ　)と(　ヒ　)の解答群(同じものを繰り返し選んでもよい)

解答番号０.　$\triangle$ＡＢＣ
　　
解答番号１.　$\triangle$ＡＩＤ

解答番号２.　$\triangle$ＢＥＦ

解答番号３.　$\triangle$ＣＧＨ

【２０２１年大問１　解答】

解答記号	解答	配点
$($ア$x + $イ$)(x - $ウ$)$	$(2x + 5)(x - 2)$	２
$\dfrac{-エ\pm \sqrt{オカ}}{キ}$	$\dfrac{-5\pm \sqrt{65}}{4}$	２
$\dfrac{ク＋ \sqrt{ケコ}}{サ}$	$\dfrac{5+ \sqrt{65}}{2}$	２
シ	$6$	２
ス	$3$	２
解答記号	解答	配点
$\dfrac{セ}{ソ}$	$\dfrac{4}{5}$	２
タチ	$12$	２
ツテ	$12$	２
ト	$2$	１
ナ	$0$	１
二	$1$	１
ヌ	$3$	３
ネ	$2$	２
ノ	$2$	２
ハ	$0$	２
ヒ	$3$	２

(大問１配点３０点　/　数学１Ａ合計配点１００点)

【２０２１年大問１　（１）解説】

「二次方程式と解」の単元からの出題で、解法は、さして難しくはありません。

しかし、計算時間を省略するためには、いくつかの解法を、選べるように訓練しておくとよいでしょう。

大問１全体で、目安時間は２０分以内です。これよりも時間がかかってしまった場合は、計算方法を工夫しましょう。

【２０２１年大問１　（１）ー（１）】

$c = 1$ のとき,　①は

$2x^2+(4 - 3)x + 2 - 1 - 11 = 0$

$2x^2+x - 10 = 0$

となります。

左辺を因数分解すると

$(2x + 5)(x - 2)$

【２０２１年大問１　（１）ー（２）】

$c = 2$ のとき,　①は

$2x^2+(8 - 3)x + 8 - 2 - 11 = 0$

$2x^2 + 5x - 5 = 0$

となります。

二次方程式の解の公式より

x = $\dfrac{-5\pm \sqrt{5^2-4\times 2\times (-5)}}{2 \times 2}$

x = $\dfrac{-5\pm \sqrt{65}}{4}$

となります。

大きい方の解を $\alpha$ とすると

$\dfrac{5}{\alpha} = 5 \div \dfrac{-5 + \sqrt{65}}{4}$

$= 5 \times \dfrac{4}{-5 + \sqrt{65}}$

$= \dfrac{20}{-5 + \sqrt{65}}$

$= \dfrac{20}{-5 + \sqrt{65}} \times \dfrac{5 + \sqrt{65}}{5 + \sqrt{65}}$　(分母の有理化)

$= \dfrac{20 \times(5 + \sqrt{65})}{-25 + 65}$

$= \dfrac{20 \times(5 + \sqrt{65})}{40}$

$= \dfrac{5 + \sqrt{65}}{2}$　(分母分子の約分)


また

$m < \dfrac{5}{\alpha} < m+1$

に $\dfrac{5}{\alpha}$ の値を代入すると

$m < \dfrac{5 + \sqrt{65}}{2} < m+1$

となります。


$\sqrt{64} < \sqrt{65} < \sqrt{81}$　なので

$8 < \sqrt{65} < 9$　

$5 + 8 < 5 + \sqrt{65} < 5 + 9$　(全辺に５を加える)

$13 < 5 + \sqrt{65} < 14$

$6.5 < \dfrac{5 + \sqrt{65}}{2} < 7$　(全辺を２で割る)

となります。


これを満たす整数 $m$ は

$6 < \dfrac{5}{\alpha} < 6 + 1$

となればよいので

$m=6$ となります。

【２０２１年大問１　（１）ー（３）】

設問文では「根号の中」と言っていますが、判別式のことですね。

①へ、判別式の公式を用いると

$(4c - 3)^2 -4 \times 2 \times (2c^2 - c - 11)$

$16c^2 -24c +9 -16c^2 +8c +88$

$-16c +97$　・・・②

となります。


②は, ①の判別式なので

②が正ならば, ①は「異なる二つの解を持つ」ことになります。

$-16c +97 > 0$

$-16c > -97$

$16c < 97$　(両辺にー１を掛ける)

$c < \dfrac{97}{16}$

$c < 6\dfrac{1}{16}$　(帯分数にする)

となります。

$c$ は正の整数なので　

$0 < c < 6\dfrac{1}{16}$

となります。


したがって、$c = 1,2,3,4,5,6$ の時

①は「異なる二つの解を持つ」ことになります。

ここで $c$ の個数を６個とすると、注意不足で、不正解となります。

「異なる二つの解を持つこと」と「解が有理数であること」は、同じことではありませんので、注意しましょう。


「解が有理数である」ためには、根号の中身に注目して、整理しましょう。

$c$	根号の中 ($-16c +97$)
1	$81=9^2$
2	$65$
3	$49=7^2$
4	$33$
5	$17$
6	$1=1^2$

したがって、根号が外れて、「解が有理数である」のは

$c = 1,3,6$ の時なので

$c$ の個数は $3$ 個である。

【２０２１年大問１　（２）解説】

「三角比」の単元からの出題で、図形には、いくつもの解法が、隠れています。

解答時間を省略するために、図形をすばやく見抜く練習をしておくとよいでしょう。

大問１全体で、目安時間は２０分以内です。これよりも時間がかかってしまった場合は、計算方法を工夫しましょう。

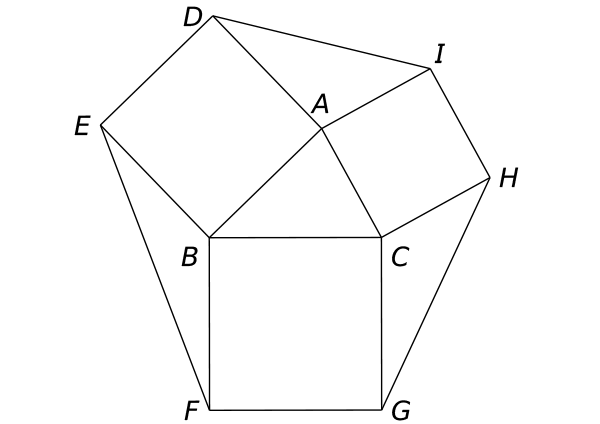
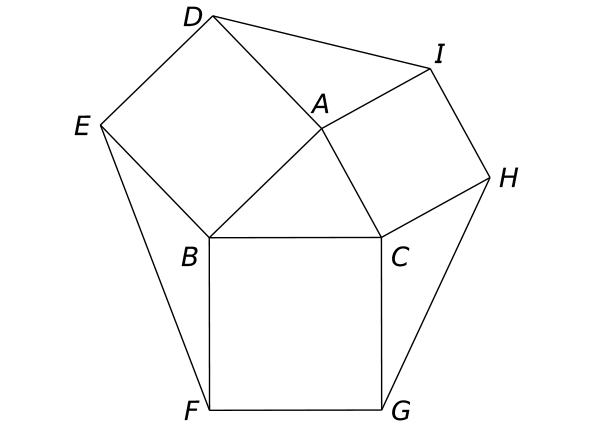
【２０２１年大問１　（２）ー（１）】

$b$＝$6$
$c$＝$5$
$cos A$＝$\dfrac{3}{5}$　のとき

三角比の公式より

$cos A^2+sinA^2=1$

が成り立つので

$(\dfrac{3}{5})^2+sinA^2 = 1$

$\dfrac{9}{25}+sinA^2 = 1$

$sinA^2 = 1 -\dfrac{9}{25}$

$sinA^2 = \dfrac{16}{25}$

$sinA = \pm\dfrac{4}{5}$

となります。


角$A$ は三角形の内角なので

$0^\circ < A < 180^\circ$

したがって

$0 < sinA < 1$

となります。


以上より

$sinA =$ $\dfrac{4}{5}$


また

$\triangle$ＡＢＣの面積は

$\triangle$ＡＢＣ=底辺 $\times$ 高さ $\times$ $\dfrac{1}{2}$

なので

点Ｃから、辺ＡＢへ、垂線を引き、交点をＮとすると



$\triangle$ＡＢＣ=ＡＢ $\times$ ＣＮ $\times$ $\dfrac{1}{2}$

=$5 \times 6sinA \times \dfrac{1}{2}$

=$5 \times 6 \times \dfrac{4}{5} \times \dfrac{1}{2}$

=$12$

となります。


また

$\triangle$ＡＩＤの面積は

=$5 \times 6sin\angle DAI \times \dfrac{1}{2} $

=$5 \times 6sin(180-A) \times \dfrac{1}{2} $



=$5 \times 6sinA \times \dfrac{1}{2} $　(三角比の関係)

=$5 \times 6 \times \dfrac{4}{5} \times \dfrac{1}{2}$

=$12$

【２０２１年大問１　（２）ー（２）】

正方形ＢＦＧＣ, ＣＨＩＡ, ＡＤＥＢの面積を

それぞれ　$S_1 ,　S_2 ,　S_3$　とする。



このとき　$S_1-S_2-S_3$　は

$S_1-S_2-S_3$=$a^2-b^2-c^2$　・・・①

となります。


余弦定理より、$\triangle$ＡＢＣについて

$a^2=b^2+c^2-2bc \cos A$　・・・②

が成り立ちます。


②を①へ代入すると

$(b^2+c^2-2bc \cos A)-b^2-c^2$

=$-2bc \cos A$


ここで $b$ と $c$ は、三角形の一辺の長さなので、必ず正の値になります。

つまり　$b, c > 0$　なので

$\cos A > 0$ ならば　$-2bc \cos A < 0$

$\cos A = 0$ ならば　$-2bc \cos A = 0$

$\cos A < 0$ ならば　$-2bc \cos A > 0$


以上より

$0^\circ < A < 90^\circ$ のとき　

すなわち　$\cos A > 0$のとき

①は負の値である



$A=90^\circ$ のとき　

すなわち　$\cos A = 0$のとき

①は $0$ である


$90^\circ < A < 180^\circ$ のとき

すなわち　$\cos A < 0$のとき

①は正の値である

【２０２１年大問１　（２）ー（３）】

$\triangle$ＡＩＤ, $\triangle$ＢＥＦ, $\triangle$ＣＧＨの面積を

それぞれ　$T_1 ,　T_2 ,　T_3$　とする。



$T_1 = \dfrac{1}{2}bc \sin(\angle ＤＡＩ)$

= $\dfrac{1}{2}bc \sin(180^\circ - A)$

= $\dfrac{1}{2}bc \sin A$　(三角比の関係)　・・・①


また

$T_2 = \dfrac{1}{2}ac \sin(\angle ＥＢＦ)$

= $\dfrac{1}{2}ac \sin(180^\circ - B)$

= $\dfrac{1}{2}ac \sin B$　(三角比の関係)　・・・②

正弦定理より

$\dfrac{a}{\sin A} = \dfrac{b}{\sin B}$

が成り立つので

$\sin B = \dfrac{b}{a} \sin A$　・・・➂

➂を、②へ代入して

$\dfrac{1}{2}ac \times \dfrac{b}{a} \sin A$

= $\dfrac{1}{2}bc \sin A$　・・・④


①=④なので

$T_1 = T_2$


また

$T_3 = \dfrac{1}{2}ab \sin(\angle ＧＣＨ)$

= $\dfrac{1}{2}ab \sin(180^\circ - C)$

= $\dfrac{1}{2}ab \sin C$　(三角比の関係)　・・・➄

正弦定理より

$\dfrac{a}{\sin A} = \dfrac{c}{\sin C}$

が成り立つので

$\sin C = \dfrac{c}{a} \sin A$　・・・⑥

⑥を、➄へ代入して

$\dfrac{1}{2}ab \times \dfrac{c}{a} \sin A$

= $\dfrac{1}{2}bc \sin A$　・・・➆


①=➆なので

$T_1 = T_3$

以上より

$a,　b,　c$　の値に関係なく $T_1=T_2=T_3$

【２０２１年大問１　（２）ー（４）】

$\triangle$ＡＢＣ, $\triangle$ＡＩＤ, $\triangle$ＢＥＦ, $\triangle$ＣＧＨのうち

外接円の半径が最も小さいものを求める。


$\triangle$ＡＢＣの, 外接円の半径を $r_0$ とおく。

正弦定理より

$\dfrac{ＢＣ}{\sin A} = 2r_0$

$r_0 = \dfrac{ＢＣ}{2\sin A}$　・・・①


また

$\triangle$ＡＩＤの, 外接円の半径を $r_1$ とおく。

正弦定理より

$\dfrac{ＩＤ}{\sin (180^\circ - A)} = 2r_1$

$\dfrac{ＩＤ}{\sin A} = 2r_1$

$r_1 = \dfrac{ＩＤ}{2\sin A}$　・・・➁

となります。


$0^\circ < A < 90^\circ$ のとき

三角形の辺と角の関係より

ＩＤ $>$ ＢＣ　

両辺を $2\sin A$ で割って

$\dfrac{ＩＤ}{2\sin A} > \dfrac{ＢＣ}{2\sin A}$

①と➁を代入して

$r_1 > r_0$

以上より

$\triangle$ＡＩＤの外接円の半径 $>$ $\triangle$ＡＢＣの外接円の半径


また

$\triangle$ＢＥＦの, 外接円の半径を $r_2$ とおく。

正弦定理より

$\dfrac{ＥＦ}{\sin (180^\circ - B)} = 2r_2$

$\dfrac{ＥＦ}{\sin B} = 2r_2$

$r_2 = \dfrac{ＥＦ}{2\sin B}$　・・・➂

となります。


$0^\circ < B < 90^\circ$ のとき

三角形の辺と角の関係より

ＥＦ $>$ ＡＣ　

両辺を $2\sin B$ で割って

$\dfrac{ＥＦ}{2\sin B} > \dfrac{ＡＣ}{2\sin B}$

正弦定理より

$\dfrac{ＥＦ}{2\sin B} > \dfrac{ＡＣ}{2\sin B}=\dfrac{ＢＣ}{2\sin A}$

①と➂を代入して

$r_2 > \dfrac{ＡＣ}{2\sin B} = r_0$


また

$\triangle$ＣＧＨの, 外接円の半径を $r_3$ とおく。

正弦定理より

$\dfrac{ＧＨ}{\sin (180^\circ - C)} = 2r_3$

$\dfrac{ＧＨ}{\sin C} = 2r_3$

$r_3 = \dfrac{ＧＨ}{2\sin C}$　・・・④

となります。


$0^\circ < C < 90^\circ$ のとき

三角形の辺と角の関係より

ＧＨ $>$ ＡＢ　

両辺を $2\sin C$ で割って

$\dfrac{ＧＨ}{2\sin C} > \dfrac{ＡＢ}{2\sin C}$

正弦定理より

$\dfrac{ＧＨ}{2\sin C} > \dfrac{ＡＢ}{2\sin C}=\dfrac{ＢＣ}{2\sin A}$

①と④を代入して

$r_3 > \dfrac{ＡＣ}{2\sin B} = r_0$


以上より

$0^\circ < A < B < C < 90^\circ$ のとき

$r_0, r_1, r_2, r_3$　のうち

$r_0$　が最も小さい

すなわち、外接円の半径が最も小さい三角形は

$\triangle$ＡＢＣである


$0^\circ < A < B < 90^\circ < C$ のとき

$r_1 > r_0$

$r_2 > r_0$

となるが

$90^\circ < C < 180^\circ$ なので

三角形の辺と角の関係より

ＧＨ $<$ ＡＢ　

両辺を $2\sin C$ で割って

$\dfrac{ＧＨ}{2\sin C} < \dfrac{ＡＢ}{2\sin C}$

正弦定理より

$\dfrac{ＧＨ}{2\sin C} < \dfrac{ＡＢ}{2\sin C}=\dfrac{ＢＣ}{2\sin A}$

①と④を代入して

$r_3 < \dfrac{ＡＣ}{2\sin B} = r_0$


以上より

$r_3 < r_0 < r_1, r_2$

となるので

外接円の半径が最も小さい三角形は$\triangle$ＣＧＨである

【共通テスト　2021年問題1　参考文献】

共通テスト2021年(令和三年) 数学

大学受験数学 過去問

大学受験数学

プロ家庭教師